CS 115 Summer 2017,

Assignment #2

Due on Thursday 6/29/2017 at 11:59PM

------------------------------------------------------------------------------------

Educational Goals: The educational goals of this program are that the student should use the concepts of

• design with pseudocode
• output of prompts and labels to match specified output
• input of values from the keyboard
• translating algebraic equations into Python expressions
• using math library functions
• calculations in assignment statements
• priority of arithmetic operations
• documentation
• testing with valid inputs and invalid inputs

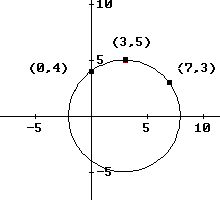
Imagine that three observers at three points on the plane are all looking at a lighthouse. They would like to know where the lighthouse is in terms of the coordinates of the plane. The lighthouse would be at the center of the circle determined by their positions.

The problem is also described as finding the equation of the circle determined by three points (as long as the three points are not all on the same straight line).

Assuming that the location of the 3 observers are given by (a, b), (c, d) and (e, f), the center (x, y) of the circle is

 

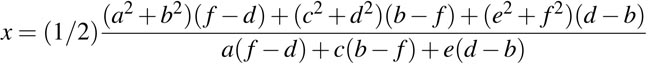
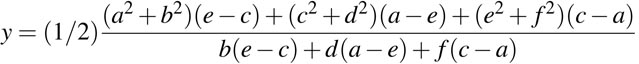
The radius of the determined circle is r. It is found using the distance formula, with one of the given points and the coordinates of the center.

Run Examples
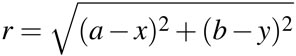
When you have the program running correctly, Verify that your program produces the same output as in the following test cases.

--- Test case 1 ---

****Lighthouse Location Calculator****

Enter the x and y of the first observer: 100, 100
Enter the x and y of the second observer: 150, 150
Enter the x and y of the third observer: 95, 125

The three observers are at
(100, 100)
(150, 150)
(95, 125)

The center of the circle is at  (130.83333333333334, 119.16666666666667)
The radius of the circle is  36.30503485131995

--- Test case 2 ---

****Lighthouse Location Calculator****

Enter the x and y of the first observer: 75, 100
Enter the x and y of the second observer: 100, 115
Enter the x and y of the third observer: 35, 80

The three observers are at
(75, 100)
(100, 115)
(35, 80)

The center of the circle is at  (-160.0, 520.0)
The radius of the circle is  481.27435003332556

--- Test case 3 ---

****Lighthouse Location Calculator****

Enter the x and y of the first observer: 7.5, 99.2
Enter the x and y of the second observer: -5, 8.99
Enter the x and y of the third observer: 15, 78

The three observers are at
(7.5, 99.2)
(-5, 8.99)
(15, 78)

The center of the circle is at  (-61.64823567957951, 62.81052983033747)
The radius of the circle is  78.1387998169119

Design

First, read the assignment carefully. Look for how the program is supposed to behave. You do not know what the code looks like - that is fine. The assignment gives some examples of normal runs. Just as in the lab exercises, decide on what steps you will need to perform to solve this problem.

# supply program prolog
# Prolog
# Author:  Mary Smith
# Email:  Mary.Smith@uky.edu
# Section: 00
# Date: 6/27/2017

'''
  Purpose: ....
  Preconditions: ....
  Postconditions: ....
'''

Requirments:

1- Use the Math fucntion from the built-in Math package

2- Your output should match the run examples above.

3- Make sure you document your program. Use good, multi-character, meaningful identifiers (variables).

4- At the top of your program, you should have a prolog (name, date, etc.) as shown a bove, and add comments explaining different operations in your code.

5- Save the program file as circle.py.

When you are done, submit your file (circle.py) as a submission for Assignment 2 on CANVAS

.