Two systems statistics computation

Definitions are below.

Enter lines of data, each specifying one edge of the bipartite graph, such as

masculine round 4
feminine round 3
masculine flat 2

full output

Definitions

We measure the discrepancy between a putative two-system scheme and a canonical two-system scheme. In order to do so, we need to first describe a canonical two-system scheme.

Say that there are two systems, A and B (such as gender and classifier). They have possible values A_1, A_2 ... (such as masculine, feminine, neuter1), and B_1, B_2 ... (such as m-classifier, f-classifier, long).

We represent type frequencies as a fraction of the whole: f(A_1), f(A_2), and so forth, where \sum_i f(A_i) = \sum_j f(B_j) = 1. So if most nouns are masculine, we might have f(A_1) = 0.8, and all the other f(A_i) values are small.

In a canonical language, we do not expect that f(A_1) = f(A_2) = ...; a canonical language might have any distribution of the frequencies, because languages represent the real world, which does not have a uniform distribution of, for instance, differently shaped objects. But we do expect a canonical language to have edge frequencies (in the bipartite graph) that respect the type frequencies. So the edge A_i B_j ought to have expected frequency e(A_i B_j) = f(A_i) \times f(B_j). In particular, we expect every possible edge to have non-zero frequency.

We denote the observed frequencies of each edge A_i B_j as o(A_i B_j). These observed frequencies might differ from the expected frequency. The discrepancy of edge A_i B_j is d(A_i B_j) = e(A_i B_j) - o(A_i B_j). Some discrepancies are negative; others are positive. The sum of all discrepancies \sum_{i,j} d(A_i B_j) = 0. Therefore, we ignore all negative discrepancies; they are exactly balanced by positive discrepancies. We therefore define the total discrepancy T = {1 \over 2} \sum_{i,j} | d(A_i B_j) |, which is equivalent to summing only the positive discrepancies.

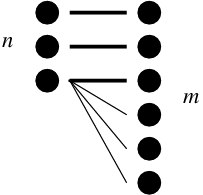
The maximum possible discrepancy when there are n values in one system and m values in the other one, where m \geq n, occurs when there are only m edges in the bipartite graph in a fashion shown in this figure:

Here, thick lines represent a large number of nouns, and thin lines represent a vanishingly small number of nouns. Such a scheme clearly has only one system, even though it poses as a two-system scheme. Simple computation shows that T = 1 - {1 \over n} - \epsilon. For example, if n = 4, the maximum possible discrepancy is T = 0.75, independent of m. We can normalize our total discrepancy measure by dividing by this maximum. So for a language that has four genders and six classifiers, we set n = 4, so the maximum possible discrepancy is 0.75. The normalized total discrepancy is N = T / {(1 - {1 \over n})} = (n T) / (n - 1). It is always a value between 0 and 1 (inclusive). A value of 0 means no discrepancy; the scheme clearly has two systems. A value of 1 means maximum discrepancy; the scheme clearly has only one system.